2022年單招數學復習題答案
一、選擇題(每題5分🔝,共28題)
題號 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
答案 |
B |
D |
B |
C |
D |
C |
A |
D |
A |
B |
B |
A |
C |
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
題號 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
答案 |
D |
A |
B |
C |
B |
C |
C |
A |
D |
C |
B |
D |
A |
B |
二📛👀、填空題(每題5分,共20題)
題號 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
答案 |
1 |
0 |
36 |
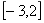
|
-4 |
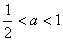
|
3 |
4 |
四 |
1 |
|
|
|
|
|
|
|
|
|
|
|
題號 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
答案 |
2 |
2 |
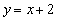
|
3 |
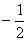
|
5 |
90° |
2 |
16 |
15 |
三👰🏼♀️👩🏻🎤、解答題(每題10分,共6題)
1.若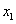 和
和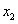 分別是一元二次方程
分別是一元二次方程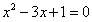 的兩根🧘🏽♀️,求
的兩根🧘🏽♀️,求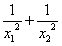 的值
的值
解:∵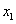 和
和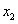 分別是一元二次方程
分別是一元二次方程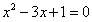 的兩根,
的兩根,
∴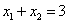 ,
,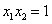 .
.
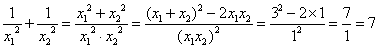
2.化簡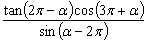
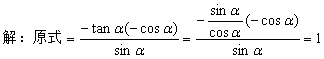
3.已知不等式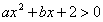 的解集為
的解集為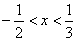 🔦,求
🔦,求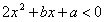 的解集?
的解集?
解:由題意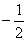 和
和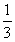 是
是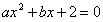 的兩個根且
的兩個根且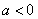 ,
,
∴ 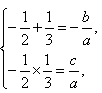 解得
解得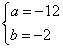 .
.
∴不等式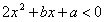 ,即為
,即為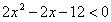 ,其解集為
,其解集為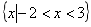 .
.
4.已知兩條平行直線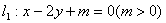 與
與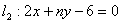 之間的距離是
之間的距離是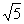 ,求m+n的值𓀙?
,求m+n的值𓀙?
解:由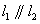 ,得
,得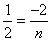 👩🏿🏫,解得
👩🏿🏫,解得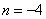 ,即直線
,即直線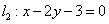 ,
,
兩直線之間的距離為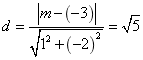 ,解得
,解得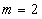 (
(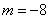 舍去),
舍去),
∴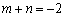
5.已知二次函數f(x)的圖像過點A(-1,0)🙋🏿♀️、B(3,0)、C(1🎠👩🏽⚖️,-8).
(1)求f(x)的解析式𓀙🚋;
(2)求f(x)在x∈[0,3]上的最值;
解:(1)由題意可設f(x)=a(x+1)(x-3),
將C(1,-8)代入得-8=a(1+1)(1-3)🖤,得a=2.
即f(x)=2(x+1)(x-3)=2x2-4x-6.
(2)f(x)=2(x-1)2-8,
當x∈[0,3]時🤲🏼,由二次函數圖像知,
f(x)min=f(1)=-8,f(x)max=f(3)=0.
6.已知函數f(x)=2cos2x-sin xcos x-2sin2x.
(1)求f(x)的最小正周期🧜🏿♂️💃🏿;
(2)求f(x)的單調區間.
解:(1)f(x)=2[(cos2x-sin2x)-2sinxcosx]=2(cos2x-sin2x)=2cos(2x+4).
∴f(x)的最小正周期T=2=π.
(2)令2kπ-π≤2x+4≤2kπ🎏,
則kπ-8≤x≤kπ-8,k∈Z.
故f(x)的單調增區間為[kπ-8,kπ-8],k∈Z.
令2kπ≤2x+4≤2kπ+π🧑🦽,
則kπ-8≤x≤kπ+8🅰️,k∈Z.
故f(x)的單調減區間為[kπ-8,kπ+8]🦌,k∈Z.
